ボーナストリガー中のビッグボーナス確率を計算してみた – スマスロ ニューパルサーBT
期待のボーナストリガー機 スマスロ ニューパルサーBTの情報が少しだけ出てきています。
今回は、確認できているボーナストリガーの性能からビッグボーナスが連続する確率などを計算してみました。
ビッグボーナスからBT突入、レギュラーを引くまで終わらない
スマスロ ニューパルサーBTは、ビッグボーナスから100％ボーナストリガーに突入し、レギュラーを引くまで終わらないループタイプとなっています。
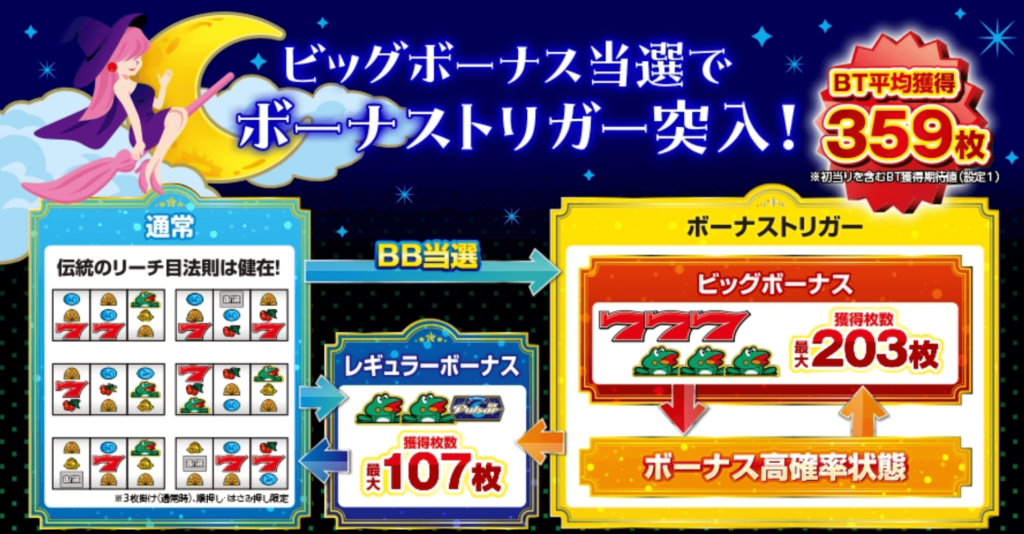
ビッグボーナスの獲得枚数が203枚、最後はレギュラーボーナスで107枚獲得できますので、ビッグボーナスは最低でも310枚の獲得が可能という嬉しい仕様になっています。
BT中のビッグボーナス確率は低そう？
ただ、公式に紹介されているBT平均獲得枚数が初回のビッグボーナス分を含めた359枚とのことですので、ビッグボーナスを連打できる可能性は低そうですね。
最低でも310枚獲得できるということは、ビッグボーナスで獲得できる余剰分は僅か49枚です。
BT中のBR比率を計算してみた
現在までに得られている情報から、BT中のBR比率を算出してみました。
といっても、今はAI時代、良くも悪くも計算なんて自分で考えるなんてことが少なくなっていく世の中です。
ここまで書いた文章から無駄を省いてAIさんにBR比率を聞いてみました。
計算系は特に、間違いを回避するために複数のAIモデルに聞いていますが、いずれのAIもビッグボーナス0.24に対しレギュラーボーナスは1という結果を返しました。
BR比率にして約2：8ということになります。
約20％でビッグボーナスを引けるようで、思ってたより引ける数値でした。
BT中に減少するメダル分を加味すれば、もう少しあるかもしれません。
この確率ならビッグボーナスの連チャンに期待しながら遊戯できますね。
ーーーー以下、AIの回答ーーー
この情報から、ボーナストリガー中のビッグボーナスとレギュラーボーナスの比率を計算してみましょう。
与えられた情報を整理すると:
初回ビッグボーナス(計算に含めない): 203枚
最後のレギュラーボーナス: 107枚
最低獲得枚数: 310枚 (初回ビッグ + 最後のレギュラー)
ボーナストリガー平均獲得枚数: 359枚 (初回ビッグボーナス分を含む)
余剰分: 49枚 (359 – 310 = 49)
この余剰分の49枚は、ボーナストリガー中に追加で発生するビッグボーナスによるものです。
1回のビッグボーナスで203枚獲得できるため:
追加ビッグボーナスの平均回数 = 49枚 ÷ 203枚 = 約0.24回
したがって、初回ビッグボーナスを除外した場合のボーナストリガー中の比率は:
追加ビッグボーナス: 約0.24回
レギュラーボーナス: 1回
ビッグボーナスとレギュラーボーナスの比率は約0.24:1となります。